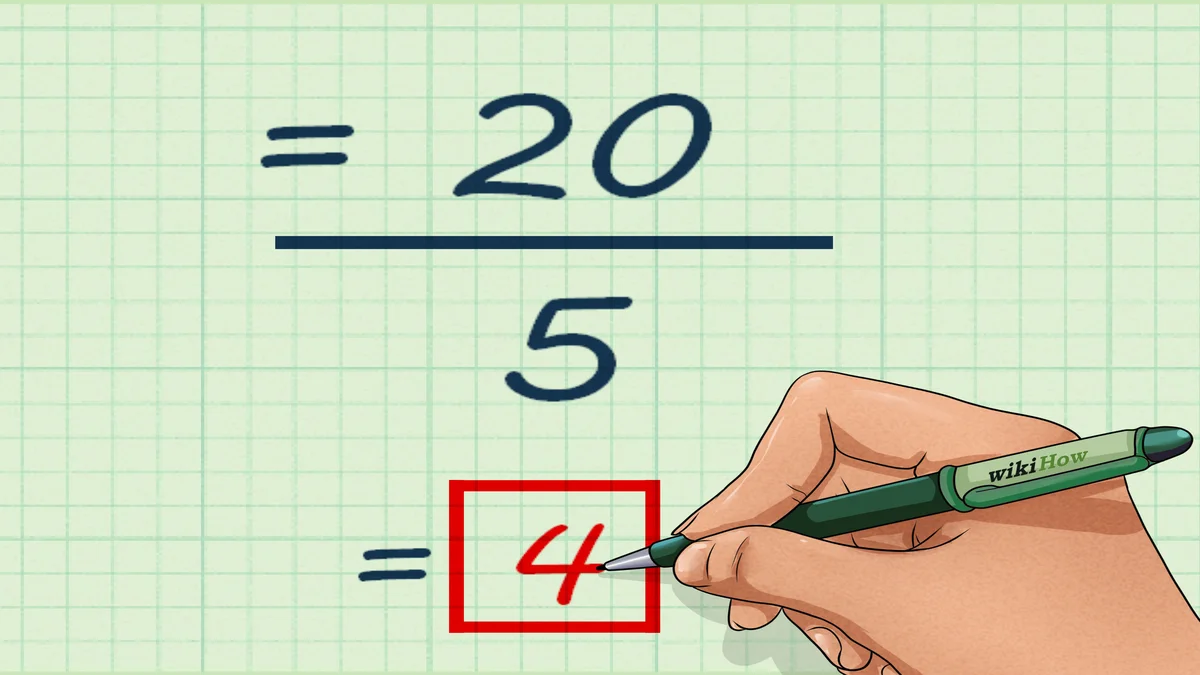دليلك الشامل حول المتوسط الحسابي : اقرأ

جدول المحتويات

يتمّ استخدام المتوسّط الحسابيّ في العديد من التّطبيقات المهمّة خلال حياتنا اليوميّة، ومنها حساب متوسّط الأعمار لفئة معيّنة من الأفراد لتحديد مستويات العناية الصحّيّة التي يتلقّونها، ويرتبط المتوسّط الحسابيّ مع بعض القيم الأخرى أيضًا لمعرفة نوع الالتواء في الرّسم البييانيّ للقيم الإحصائيّة، ويُعرف المتوسّط بأنّه مجموع القيم على عددها.

يتحدث هذا المقال عن نظرية المتوسط الحسابي، ويشمل:

ذكر تعريف المتوسّط الحسابيّ مع تزويد القارئ بالمعادلة الرّياضيّة لحساب المتوسّط.
الإشارة إلى علاقة المتوسّط الحسابيّ بتحديد نوع الالتواء في الرّسم البيانيّ.
ذكر العديد من الأمثلة على المتوسّط الحسابيّ لمجموعة من القيم.
الإشارة إلى طريقة حساب المتوسّط الحسابيّ للجدول التّكراريّ مع أمثلة على ذلك.

ما هو المتوسط الحسابي ؟

يُعرف المتوسّط الحسابيّ في الرّياضيّات بأنّه قيمة رياضيّة تتجمّع حولها العديد من القيم الرّياضيّة الأُخرى، إلّا أنّ هذا المتوسّط الحسابيّ غير مناسب في كثير من الحقول، ومنها: حقل الأموال؛ فإنّ قيمة شاذّة واحدة تؤثّر على المتوسّط الحسابيّ بشكل كبير، ويُستخدم المتوسّط الحسابيّ المذكور في العديد من المجالات، وأبرزها الإحصاء.

قانون المتوسط الحسابي

إنّ المتوسّط الحسابيّ يساوي مجموع القيم مقسومًا على عددها، ويُمكننا كتابة هذا القانون على الصّورة M=1n i=1nxi=1n(x1+x2+……..+xn) وتشير الرّموز في هذا القانون إلى الآتي:

n: يشير إلى مجموع عدد القيم التي نريد معرفة الوسط الحسابيّ لها.
x: يشير في القانون السّابق إلى القيم التي نريد معرفة وسطها الحسابيّ.
M: يشير إلى قيمة المتوسّط الحسابيّ.

كيفية حساب المتوسط الحسابي

حساب الوسط الحسابي لمجموعة من الأعداد

يتمّ حساب المتوسّط الحسابيّ لمجموعة من الأعداد عن طريق قسمة مجموع قيمها على عددها كما يأتي:

تحديد مجموعة الأرقام التي نريد معرفة متوسّطها الحسابيّ؛ على أن تكون أرقامًا حقيقيّة لا مُتغيّرات.
جمع الأرقام السّابقة مع بعضها البعض، ثمّ استخراج نتيجة عمليّة الجمع.
حساب عدد الأرقام التي جمعنا قيمتها سابقًا بغضّ النّظر عن قيمة كلّ واحدة منها.
قسمة نتيجة عمليّة الجمع الأولى على ناتج عمليّة الجمع الثانية لمعرفة المتوسّط الحسابيّ.

حساب الوسط الحسابي للجداول التكرارية

تحتوي الجداول التّكراريّة على العديد من البيانات التي تُمثّل القيمة العدديّة مع مرّات تكرارها، ويتمّ حساب المتوسّط الحسابيّ لهذه الجداول بطريقة مشابهة لطريقة حساب المتوسّط لمجموعة من الأعداد، إلّا إنّ عدد القيم يختلف بشكل كبير، وفيما يأتي مثالٌ يوضّح طريقة معرفة المتوسّط الحسابيّ للجداول التّكراريّة:

الفئة	عدد مرات التّكرار
20-26	10
50-58	16
63-67	12
46-50	17
51-55	8
30-34	19

معرفة المتوسّط الحسابيّ لكلّ فئة من الفئات السّابقة كما يأتي:
- (26+20)/2=23
- (58+50)/2=54
- (67+63)/2=65
- (50+46)/2=48
- (55+51)/2=53
- (34+30)/2=32
ضرب المتوسط الحسابي لكلّ فئة بعدد مرات التّكرار:
- 23×10=230
- 54×16=864
- 65×12=780
- 48×17=816
- 53×8=424
- 32×19=608
جمع نواتج عمليات الضرب السابقة مع بعضها البعض:
- 230+864+780+816+424+608=3,722
معرفة عدد مرات التكرار الكلية في الجدول كما يأتي:
- 10+16+12+17+8+19=82
قسمة النّتيجتين الأخيرتين على بعضهما كما يأتي:
- 3,722÷82=45,39 تقريبًا.

دالة المتوسط الحسابي في excel

تساعدنا دالّة المتوسّط الحسابيّ AVERAGE في برنامج الجداول الشّهير excel على معرفة المتوسّط مباشرة بعد إدخال القيم الرّياضيّة في حقول البرنامج، ونستطيع الاستفادة من هذه الدّالة كما يأتي:

كتابة جميع القيم الذي نريد معرفة وسطها الحسابيّ في حقول excel مع إفراد كلّ قيمة في حقل مُستقلّ.
الضّغط على أحد الحقول الفارغة بعد إدخال جميع القيم المطلوبة.
كتابة رمز المساواة = ثمّ إدخال كلمة AVERAGE، والضّغط عليها نقرًا مزدوجًا بزرّ الفأرة الأيمن من القائمة المُنسدلة.
تحديد جميع القيم التي تمّ إدخالها، ثمّ الضّغط على زرّ الإدخال Enter لإظهار قيمة المتوسّط الحسابيّ مباشرة.

اقرأ أيضاً: المركبات الحلقية

العلاقه بين المتوسط الحسابي والوسيط والمنوال في تحديد نوع الالتواء

توجد العديد من الطّرق التي يُمكن اتّباعها لتحديد نوع الالتواء، وأبرزها الطّريقة التي تعتمد على العلاقة بين قيمة المتوسّط الحسابيّ إلى جانب الوسيط والمنوال، وذلك من خلال المعادلة الآتية:

α=3×(x-Med)S

تشير رموز هذه المعادلة إلى الآتي:

الرّمز α: يشير إلى معامل الالتواء لبيرسون.
الرّمزx: يشير إلى المتوسّط الحسابيّ لمجموع الأرقام.
الرّمز Med: تشير الحروف Med إلى الوسيط الحسابيّ.
الرّمز S: يشير إلى الانحراف المعياريّ الذي يُعرف باسم المنوال.

يمكننا معرفة نوع الالتواء بناءً على قيمة α كما يأتي:

يكون منحنى التّوزيع المعياريّ متماثلًا دون التواء عندما تكون قيمة ألفا α=صفر.
إذا كانت قيمة ألفا α أكبر من صفر كان المُنحنى ملتويًا إلى اليمين.
إذا كانت قيمة ألفا α أكبر من صفر كان المُنحنى ملتويًا إلى اليسار.

مسائل على المتوسط الحسابي

ما هو المتوسط الحسابيّ لمجموعة القيم الآتية: 5، 10، 16، 25، 16، 19، 14، 17؟
- نجمع القيم السّابقة مع بعضها البعض: 5+10+16+25+16+19+14+17=122
- نحسب عدد القيم السابقة، وهو العدد 5.
- نجد المتوسّط الحسابيّ كما يأتي: 122÷5=24.4
كيف يُمكننا حساب المتوسّط الحسابيّ للجدول التّكراريّ الآتي؟

الفئة	عدد مرّات التّكرار
50-56	15
89-93	17
20-28	13
63-71	10
41-53	18
62-64	14

إيجاد المتوسّط الحسابيّ لكلّ فئة من الفئات السّابقة:
- (50+56)÷2=53
- (89+93)÷2=91
- (20+28)÷2=24
- (63+71)÷2=67
- (41+53)÷2=47
- (62+64)÷2=63
ضرب كلّ متوسّط حسابيّ بعدد التّكرارات:
- 53×15=795
- 91×17=1,547
- 24×13=312
- 67×10=670
- 47×18=846
- 63×14=882
إيجاد مجموع القيم السّابقة:
- 795+1,547+312+670+846+882=5,052
إيجاد مجموع تكرار الفئات في الجدول:
- 15+17+13+10+18+14=87
تقسيم القيمتين الأخيرتين على بعضهما كما يأتي: 5,052÷87=58,06 تقريبًا.

طريقة حساب متوسط الدخل الشهري

يتمّ حساب متوسّط الدّخل الشّهريّ السّنويّ عن طريق قسمة مجموع الرّواتب التي تقاضاها الموظّف خلال السّنة كاملة على عدد الأشهر في السّنة الواحدة، وهو 12 شهر، وفيما يأتي مثال لحساب متوسّط الدّخل الشّهريّ للموظّف:

اقرأ أيضاً: ما هي طريقة تحويل رصيد آسيا

الدخل الشهري	الشهر
1,300 دولار	يناير
1,250 دولارًا	فبراير
1,350 دولارًا	مارس
1,200 دولار	أبريل
1,300 دولار	مايو
1,250 دولارًا	يونيو
1,400 دولار	يوليو
1,350 دولارًا	أغسطس
1,250 دولارًا	سبتمبر
1,200 دولار	أكتوبر
1,350 دولارًا	نوفمبر
1,200 دينار	ديسمبر

إيجاد مجموع قيمة الرّواتب السّابقة:
- 1,300+1250+1,350+1,200+1,300+1,250+1,400+1,350+1,250+1,200+1,350+1,200=15,400 دولار
قسمة النّاتج السابق على عدد الأشهر كما يأتي:
- 15,400÷12=1,283.33 دولار

كيفية حساب المتوسط الحسابي والانحراف المعياري للاستبيان

تتمّ معرفة المتوسّط الحسابيّ للاستبيان عن طريق قسمة مجموع قيم البيانات على عددها كما يأتي:

تحديد البيانات التي نرغب بمعرفة متوسّطها الحسابيّ، ثمّ استخراج مجموعها.
حساب عدد القيم التي تضمّ البيانات السابقة.
قسمة مجموع القيم على عدد القيم لمعرفة المتوسّط الحسابيّ.

لا بُدّ من استخدام المعادلة 2in(x-x)2n-1من أجل حساب الانحراف المعياريّ لقيم الاستبيان، وتُمثّل رموز هذه المعادلة ما يأتي:

الرّمزx: يشير هذا الرّمز إلى قيمة المتوسّط الحسابيّ.
الرّمز x: يشير إلى القيم المشمولة في الدّراسة.
الرّمز n: يشير إلى عدد القيم التي تشملها الدّراسة.

كيفية حساب متوسط الأجر الشهري لآخر سنتين

يتمّ حساب متوسّط الأجر الشهريّ خلال سنتين عن طريق جمع الرّواتب مع بعضها البعض، ثمّ قسمتها على 24 شهرًا كما في المثال الآتي:

الراتب الشهري	الشهر
1,500 دولار	يناير
1,250 دولارًا	فبراير
1,300 دولار	مارس
1,650 دولارًا	أبريل
1,400 دولار	مايو
1,450 دولارًا	يونيو
1,300 دولار	يوليو
1,250 دولارًا	أغسطس
1,300 دولار	سبتمبر
1,400 دولار	أكتوبر
1,400 دولار	نوفمبر
1,450 دولارًا	ديسمبر
1,500 دولار	يناير
1,550 دولارًا	فبراير
1,350 دولارًا	مارس
1,450 دولارًا	أبريل
1,350 دولارًا	مايو
1,200 دولار	يونيو
1,400 دولار	يوليو
1,500 دولار	أغسطس
1,400 دولار	سبتمبر
1,350 دولارًا	أكتوبر
1,250 دولارًا	نوفمبر
1,450 دولارًا	ديسمبر